5. Ferramentas de Econometria
O Macrodados oferece recursos de estatística e econometria fundamentais para a elaboração de modelos econométricos e projeções :
- Estatísticas descritivas
- Correlação e correlograma
§ Correlações, autocorrelações, autocorrelações parciais
- Correlograma, estatística Q de Ljung-Box
- Regressão linear múltipla
§ Coeficientes, erros padrão, estatísticas, erros auto-regressivos
- Gráficos da série ajustada e do resíduo, matriz de covariância
- Testes de especificação e diagnóstico
§ Testes de coeficientes
- Testes de resíduos
- Testes de estabilidade
- Filtro de Hodrick-Prescott
- Teste de raiz unitária ADF
o Teste Granger-Causalidade
- X12-ARIMA
5.1 Estatísticas descritivas
Esta opção apresenta um conjunto de estatísticas descritivas para uma série e permite a geração de um histograma da distribuição de freqüência.
Para acessar clique em Econometria no menu principal e a seguir clique em Estatísticas descritivas, como na figura abaixo :
A seguir a descrição das estatísticas disponíveis neste recurso :
|
Média |
Valor médio da série (sensível a outliers) |
x = å xt / N |
|
Moda |
Ponto central da classe de maior freqüência. Varia de acordo com o número de classes. |
Valor central da classe mais freqüente. |
|
Mediana |
Ponto central da distribuição (pouco sensível a outliers) |
Valor central (ou média entre os dois pontos centrais se o número de observações for par) |
|
Máximo e Mínimo |
Máximo (o maior) e mínimo (o menor) valor da série na amostra. |
Maior e menor valor. |
|
Variância |
Medida de dispersão da série em relação à média |
å (xt - x)2/(N-1) = S2 |
|
Desvio padrão |
Raiz quadrada da variância = S. É uma medida de dispersão com dimensão comparável a da média, ou seja, está expresso na mesma unidade da série. |
S |
|
Coeficiente de variação
|
Medida de dispersão relativa normalizada pela média. |
S/x |
|
Coeficiente de assimetria |
Medida da assimetria da distribuição. Na distribuição normal, simétrica, o coeficiente A é igual a zero. Um coeficiente A maior que zero indica uma cauda direita alongada. Se menor que zero indica uma cauda esquerda alongada. |
A = (1/N) * [S ( (xt – x) / se ) 3 ] onde se= S*((N-1)/N)1/2 é a estimativa do desvio padrão sem correção para o viés de amostragem
|
|
Curtose
|
Medida do achatamento da distribuição. Na distribuição normal K é igual a 3. Se K for maior que 3 a distribuição é menos achatada que a normal. Se K for menor que 3 a distribuição é mais achatada. |
K = (1/N)*[S ( (xt – x) / se ) 4 ] |
|
Estatística para testar se a série tem distribuição normal, baseada em diferenças entre assimetria e curtose da distribuição da série em relação à normal |
JB = (N/6)*( A2 + (K-3)2 /4 |
|
|
É a probabilidade de não rejeitar a hipótese de normalidade. Se este valor for suficientemente pequeno, pode-se rejeitar a hipótese de normalidade. |
Prob(Qui-quadrado com 2 graus de liberdade) |
A probabilidade JB mostrada na janela de saída do teste é a probabilidade de que a estatística Jarque-Bera exceda (em valor absoluto) o valor observado se a hipótese nula de normalidade for verdadeira.
ü Uma probabilidade JB pequena (isto é, um valor próximo de zero) significa que a hipótese de normalidade deve ser rejeitada.
No exemplo a seguir, existe probabilidade de 94.73% (100*(1-0,0573)) de que a distribuição não seja normal, ou seja, a hipótese de normalidade deve ser rejeitada.
Também podemos concluir que a distribuição é ligeiramente assimétrica à esquerda e um pouco mais achatada que a da normal padrão.
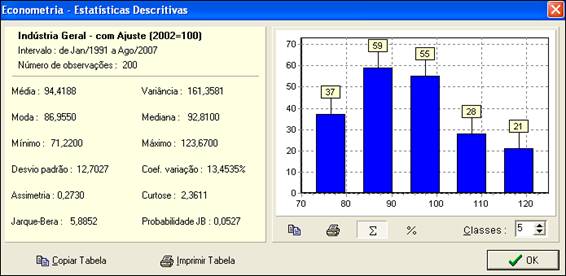
A tabela com as estatísticas da série pode ser copiada para outros programas, tais como Microsoft Word ou Excel, ou impressa.
Para isso clique em ![]() ou em
ou em ![]() .
.
O histograma (gráfico) da figura divide os valores da amostra (série) em um determinado número de classes (sub-intervalos) e indica o número de observações da série para cada classe.
Cada barra corresponde ao número de observações da série que se encontra na classe correspondente. No topo das barras são indicadas quantas observações da série existem no sub-intervalo (classe) correspondente.
Para aumentar o número de classes altere o valor em ![]() .
.
Para copiar ou imprimir o histograma clique em ![]() ou em
ou em ![]() .
.
Para visualizar no histograma os percentuais das
classes clique em ![]() .
.
5.2 Filtro de Hodrick-Prescott
O Filtro de Hodrick-Prescott é um método criado pelos economistas Robert Hodrick e Edward Prescott para obter uma série de tendência não linear suavizada.
É uma técnica muito usada em ciclos reais de negócios, para extrair a tendência de séries como a do PIB por exemplo. A série filtrada é mais sensível a flutuações de longo prazo do que de curto prazo. O ajuste de sensibilidade é feito no parâmetro de amortecimento l descrito a seguir.
Seja Yt o logaritmo da série original para t=1, 2, ..., T. Considere que a série Y possui um componente de tendência t e um componente cíclico C, de modo que : Yt = tt + Ct
Existe um componente de tendência que minimiza a equação a seguir, para um dado valor positivo do parâmetro l :
T T-1
MIN å (Yt – tt) 2 + å [ (tt+1 – tt ) – (tt – tt-1) ]2
t=1 t=2
O primeiro termo da equação é a soma dos desvios ao quadrado, que penaliza o componente cíclico. O segundo termo penaliza variações na taxa de crescimento do componente de tendência. Quanto maior for o valor do parâmetro de amortecimento l maior é a penalidade.
Recomenda-se usar um parâmetro l de 14400 para séries mensais, 1600 para trimestrais e 100 para anuais.
O Filtro de Hodrick-Prescott está disponível no Macrodados no menu principal, em Econometria, como mostrado na figura a seguir.
Ao ser acionada, esta opção mostra uma janela que solicita a série a ser filtrada e o parâmetro de amortecimento. É possível também restringir o intervalo a ser considerado informando-se as datas inicial e final nos campos correspondentes.
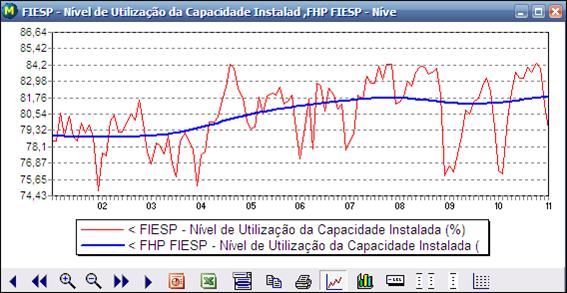
Se apenas uma série for selecionada com o campo Gráfico marcado, será também mostrado um gráfico com a série original e a série filtrada.
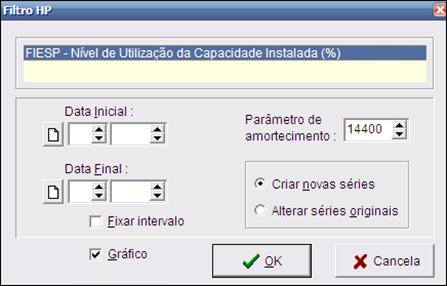
Após clicar em Ok, o programa gera uma nova série e mostra o gráfico. A nova série tem o prefixo FHP.
5.3 Correlograma
Use esta opção para ver uma tabela numérica e um gráfico das autocorrelações e autocorrelações parciais de uma série.
A autocorrelação de uma série Y na defasagem K é definida por :
T T
AC(K) = å [(Yt - xy)*( Yt-k - xy)] / å [(Yt - xy)2]
K+1 1
, onde xy é a média de Y
A autocorrelação é o coeficiente de correlação para valores da série separados por K períodos. Quando K é igual a zero o resultado é igual a 1.
q Se AC(1) for diferente de zero então a série tem correlação serial de primeira ordem.
q Se AC(K) diminui mais ou menos geometricamente quando K aumenta, é um sinal que a série segue um processo auto-regressivo (AR).
q Se AC(K) cai a zero após um número pequeno de lags, é um sinal que a série segue um processo de médias móveis de baixa ordem (MA).
Para obter o correlograma, clique em Econometria – Correlograma, no menu principal.
Será mostrada uma janela como na figura abaixo :
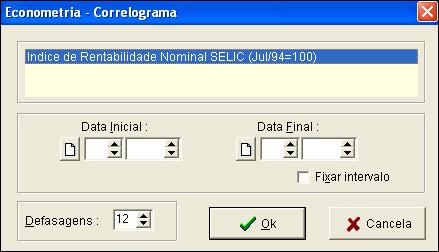
Os campos Data Inicial e Data Final podem ser usados para definir o intervalo a ser considerado no correlograma. Se estes campos forem deixados em brando será considerado o intervalo completo da série.
Os ícones ao lado dos campos de data servem para apagar a data indicada e assim considerar a observação mais antiga (Data Inicial) ou mais recente (Data Final).
O campo Defasagem indica o numero de defasagens a ser mostrado no correlograma.
Selecione a opção Fixar intervalo se desejar manter um determinado intervalo para os próximos correlogramas.
As linhas tracejadas no gráfico das autocorrelações correspondem aos limites de dois desvios padrão.
Ø Se a autocorrelação estiver contida nestes limites então ela não é significantemente diferente de zero ao nível aproximado de 5% de significância.
A autocorrelação parcial de uma série Y na defasagem K, ACP(K), é estimada como sendo o coeficiente da regressão associado à variável independente Yt-k considerando o seguinte modelo de regressão :
Yt = cte + a1* Yt-1 + a2* Yt-2 + … + aK* Yt-k
ACP(K) = aK
Ela é dita parcial porque mede a correlação entre observações separadas por K períodos, após remover o efeito das defasagens intermediárias.
Para séries temporais, uma grande parte da correlação entre Yt e Yt-k pode ser devida às correlações com as defasagens Yt-1 ,Yt-2 ,..., Yt-k-1 . A autocorrelação parcial remove a influência destes termos.
Ø Se o padrão da autocorrelação pode ser descrito como de ordem menor que K então a autocorrelação parcial na defasagem K será próxima de zero.
A análise das autocorrelações e das autocorrelações parciais deve levar em conta a estatística Q de Ljung-Box.
Esta estatística é aproximadamente distribuída como uma Qui-quadrado com K graus de liberdade se :
Hipótese nula : Não existe autocorrelação até a ordem K
A coluna Prob mostra a probabilidade que a estatística Q seja significante.
ü Um valor pequeno de Prob sugere a rejeição da hipótese nula. Por exemplo, um valor de Prob menor que 0,05 indica que a probabilidade que exista autocorrelação até a ordem K é de 95%.
Os campos Data Inicial e Data Final podem ser usados para definir o intervalo da amostra.
Se não preenchidos o programa considera o maior intervalo que contenha todas as observações disponíveis das séries.
O campo Intervalo indica o número máximo de defasagens que serão considerados.
Uma vez selecionadas as séries de interesse, clique em Ok para processar. A figura abaixo ilustra um correlograma para a série mensal de Índice de Rentabilidade da SELIC :
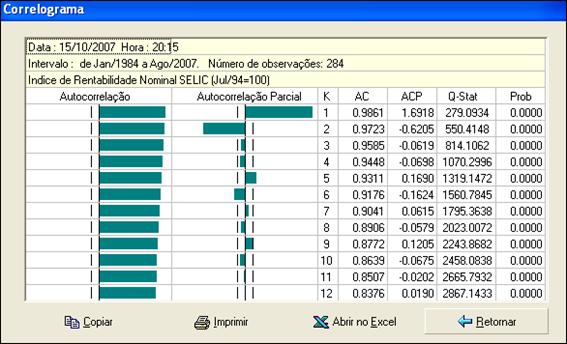
Para copiar a saída para outros ambientes, imprimir a tabela ou abrir o correlograma no Excel, use os botões :
![]() ,
,
![]() ou
ou ![]() .
.
5.4 Correlograma cruzado
Considere duas séries X e Y. Dado que :
Variância de X : Var(X) = å (xi - xx)2/(N-1)
Variância de Y : Var(Y) = å (yi - xy)2/(N-1)
, onde xx e xy são as médias de X e Y.
Define-se a Covariância entre X e Y como sendo :
Cov(X,Y) = å [(xi - xx)*( yi - xy)]/(N-1)
A covariância dá uma medida de dispersão conjunta das duas séries. A partir daí deriva-se o conceito de correlação, que dá uma medida do grau de associação entre as duas séries.
Cor(X,Y) = Cov(X,Y) / [ Var(X)*Var(Y) ] =
å [(xi - xx)*( yi - xy)] / [(å (xi - xx))1/2*(å (yi - xy)) ½]
É fácil verificar que:
–1 <= Cor(X,Y) >= 1.
q Uma correlação positiva indica que o valor de Y tende a aumentar sempre que o valor de X aumenta.
q Uma correlação negativa indica que o valor de Y tende a diminuir sempre que o valor de X aumenta.
q Um valor zero indica que as séries não são correlacionadas, ou seja, a variação de X não afeta a variação de Y.
As linhas tracejadas no gráfico das correlações correspondem aos limites de dois desvios padrão.
Se a correlação estiver contida nestes limites então ela não é significantemente diferente de zero ao nível aproximado de 5% de significância.
O correlograma cruzado do Macrodados mostra a correlação entre X e Y e também as correlações entre X e as defasadas de Y e entre X e as adiantadas de Y.
Ao ser acionada esta opção mostra a janela da figura abaixo :
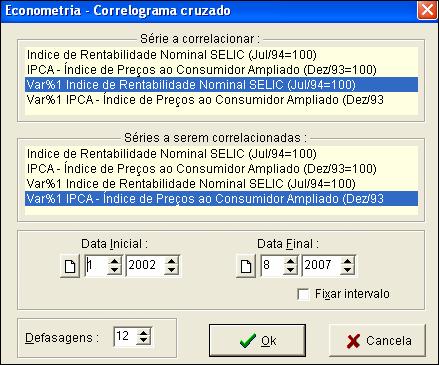
Os campos Data Inicial e Data Final podem ser usados para definir o intervalo da amostra. Se não preenchidos o programa considera o maior intervalo que contenha todas as observações disponíveis das séries.
Para o exemplo considerado obtém-se o seguinte correlograma cruzado :
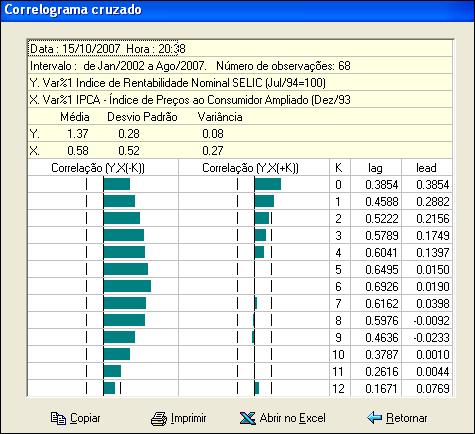
No exemplo da figura o correlograma indica que a variação da SELIC é mais fortemente correlacionada com a variação do IPCA defasada de 6.
Para copiar a saída para outros ambientes, imprimir a tabela ou abrir o correlograma no Excel, use os botões :
![]() ,
,
![]() ou
ou ![]() .
.